BCA 4th Sem - Boundary Representations

• UNIT-I 

~The Advantages of Interactive Graphics
~Representative Uses of Computer Graphics 
~Classification of Application Development of Hardware and software for computer Graphics
~Overview, Scan:
~Converting Lines
~Scan Converting Circles
~Scan Converting Ellipses

UNIT-II 

~Hardcopy Technologies
~Display Technologies
~Raster-Scan Display System
~Video Controller
~Random-Scan Display processor
~Input Devices for Operator Interaction
~Image Scanners
~Working exposure on graphics tools like Dream Weaver, 3D Effects etc
~Clipping
~Southland- Cohen Algorithm
~Cyrus-Beck Algorithm
~Midpoint Subdivision Algorithm

UNIT-III 

~Geometrical Transformation
~2D Transformation
~Homogeneous Coordinates and Matrix Representation of 2DTransformations 
~composition of 2D Transformations
~The Window-to-Viewport
Transformations

~Introduction to 3D Transformations Matrix

UNIT-IV 

Representing Curves & Surfaces----

Polygon meshes parametric

Cubic Curves

Quadric Surface

Solid Modeling   Representing Solids

Regularized Boolean Set Operation primitive Instancing Sweep   Representation
Boundary Representations
Spatial Partitioning Representations
Constructive Solid Geometry Comparison of Representations

UNIT-V                           

~Multimedia Definition
~CD-ROM and the multimedia highway
~Computer Animation
(Design, types of animation, using different functions)

UNIT-VI  

~Uses of Multimedia
~Introduction to making multimedia –
~The stage of Project
~hardware & software requirements to make good multimedia skills
~Training opportunities in Multimedia Motivation for Multimedia usage

Boundary Representations

Boundary Representation, or B-rep for short, can be considered as an extension to the wireframe model. The merit of a B-rep is that a solid is bounded by its surface and has its interior and exterior. 

The surface of solid consists of a set of well-organized faces, each of which is a piece of some surface (.e.g., a surface patch). Faces may share vertices and edges that are curve segments. Therefore, a B-rep is an extension of the wireframe model by adding face information to the latter.

There are two types of information in a B-rep: 

1. topological
2.  geometric.

 Topological information provides the relationships among vertices, edges, and faces similar to that used in a wireframe model. In addition to connectivity, topological information also includes the orientation of edges and faces. 

Geometric information is usually equations of the edges and faces.

• The geometry of a vertex is just its position in space as given by its (x,y,z) coordinates.
• Edges may be straight lines, circular arcs, etc..
• A face is represented by some description of its surface (algebraic or parametric forms used).

  Boundary Representation (B-rep)

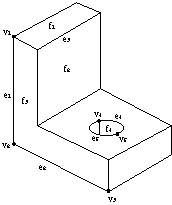
Validity Check Using Euler-Poincare Example

Given the boundary representation solid shown, verify the Euler-Poincare relationship.

The Euler equation provides an invariant relationship between the vertices, edges, and

surfaces of a simple polyhedral object. The Euler-Poincare equation expands this relation to

include objects with holes, passages, etc.

For the object at right:

Vertices = 24

Edges = 36

Faces = 14

Make sure to look at ALL the faces that bound the volume, then find the bounding edges for

those faces and finally the vertices associated with the edges. Check your count twice. Don’t forget that the rounds require their own surface definitions.

Genus = 1 (one through passage)

Shell = 1 (no internal void)

(Hole) Loops = 2

Solving the Euler-Poincare equation:

V – E + F – L       = 2 (S – G)

24 – 36 + 14 – 2 = 2 (1 – 1)

                            0 = 0

Next TopicSpatial Partitioning Representations

← prevnext →