BCA 4th Sem-Southland- Cohen Algorithm

• UNIT-I 
~The Advantages of Interactive Graphics
~Representative Uses of Computer Graphics 
~Classification of Application Development of Hardware and software for computer Graphics
~Overview, Scan:
~Converting Lines
~Scan Converting Circles
~Scan Converting Ellipses








UNIT-II 
~Hardcopy Technologies
~Display Technologies
~Raster-Scan Display System
~Video Controller
~Random-Scan Display processor
~Input Devices for Operator Interaction
~Image Scanners
~Working exposure on graphics tools like Dream Weaver, 3D Effects etc
~Clipping
~Southland- Cohen Algorithm
~Cyrus-Beck Algorithm
~Midpoint Subdivision Algorithm






UNIT-III 
~Geometrical Transformation
~2D Transformation
~Homogeneous Coordinates and Matrix Representation of 2DTransformations 
~composition of 2D Transformations
~The Window-to-Viewport
Transformations

~Introduction to 3D Transformations Matrix





UNIT-IV 
Representing Curves & Surfaces----
Polygon meshes parametric
Cubic Curves
Quadric Surface
Solid Modeling   Representing Solids
Regularized Boolean Set Operation primitive Instancing Sweep   Representation
Boundary Representations
Spatial Partitioning Representations
Constructive Solid Geometry Comparison of Representations





UNIT-V                           


~Multimedia Definition
~CD-ROM and the multimedia highway
~Computer Animation
(Design, types of animation, using different functions)





UNIT-VI  


~Uses of Multimedia
~Introduction to making multimedia –
~The stage of Project
~hardware & software requirements to make good multimedia skills
~Training opportunities in Multimedia Motivation for Multimedia usage

Southland- Cohen Algorithm

In the calculation, most importantly, it is recognized whether the line lies inside the screen or it is outside the screen. All lines go under any of the accompanying classifications: 

1. Visible
2. Not Visible
3. Clipping Case

1. Visible: If a line exists in the window, i.e., the two endpoints of the line exists in the window. A line is noticeable and will be shown for what it's worth. 

2. Not Visible: If a line lies outside the window it will be undetectable and dismissed. Such lines won't show. In the event that anybody of the accompanying imbalances is fulfilled, at that point, the line is viewed as imperceptible. Let A (x1,y2) and B (x2,y2) are endpoints of line.

x_min,x_max are coordinates of the window.

y_min,y_max are also coordinates of the window.
          x₁>x_max
          x₂>x_max
          y₁>y_max
          y₂>y_max
          x₁<x_min
          x₂<x_min
          y₁<y_min
          y₂<y_min

3. Clipping Case: If the line is neither noticeable case nor imperceptible case. It is viewed as a cut case. Above all else, the class of a line is discovered dependent on nine locales given underneath. Every one of the nine locales is doled out codes. Each code is of 4 bits. In the event that the two endpoints of the line have end bits zero, at that point the line is viewed as obvious.

next →← prev Line Clipping: It is performed by using the line clipping algorithm. The line clipping algorithms are: Cohen Sutherland Line Clipping Algorithm Midpoint Subdivision Line Clipping Algorithm Liang-Barsky Line Clipping Algorithm Cohen Sutherland Line Clipping Algorithm: In the algorithm, first of all, it is detected whether line lies inside the screen or it is outside the screen. All lines come under any one of the following categories: Visible Not Visible Clipping Case 1. Visible: If a line lies within the window, i.e., both endpoints of the line lies within the window. A line is visible and will be displayed as it is. 2. Not Visible: If a line lies outside the window it will be invisible and rejected. Such lines will not display. If any one of the following inequalities is satisfied, then the line is considered invisible. Let A (x1,y2) and B (x2,y2) are endpoints of line. xmin,xmax are coordinates of the window. ymin,ymax are also coordinates of the window.           x1>xmax           x2>xmax           y1>ymax           y2>ymax           x1<xmin           x2<xmin           y1<ymin           y2<ymin 3. Clipping Case: If the line is neither visible case nor invisible case. It is considered to be clipped case. First of all, the category of a line is found based on nine regions given below. All nine regions are assigned codes. Each code is of 4 bits. If both endpoints of the line have end bits zero, then the line is considered to be visible. 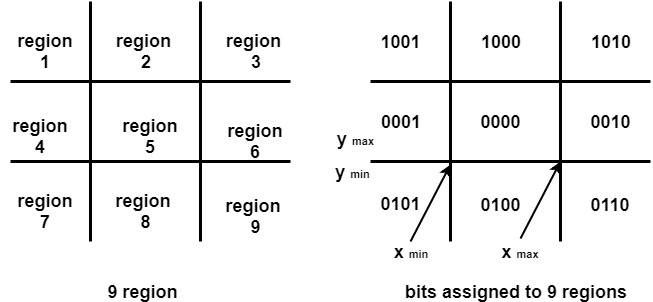The center area is having the code, 0000, i.e., region 5 is considered a rectangle window.

show lines of various types

Line AB is the visible case

Line OP is an invisible case

Line PQ is an invisible line

Line IJ are clipping candidates

Line MN are clipping candidate

Line CD are clipping candidate

Algorithm of Cohen Sutherland Line Clipping:

Step1: Calculate positions of both endpoints of the line

Step2: Perform OR operation on both of these end-points

Step3: If the OR operation gives 0000
       Then
                the line is considered to be visible
       else
          Perform AND operation on both endpoints
      If And ≠ 0000
          then the line is invisible
        else
      And=0000
    The line is considered the clipped case.

Step4: If a line is clipped case, find an intersection with boundaries of the window
                m=(y₂-y₁ )(x₂-x₁)

(A) If bit 1 is "1" line intersects with the left boundary of the rectangle window
                y₃=y₁+m(x-X₁)
                where X = X_wmin
                where X_wminis the minimum value of X co-ordinate of window

(B) If bit 2 is "1" line intersects with right boundary
                y₃=y₁+m(X-X₁)
                where X = X_wmax
                where X more is the maximum value of X coordinate of the window

(C) If bit 3 is "1" line intersects with bottom boundary
                X₃=X₁+(y-y₁)/m
                      where y = y_wmin
                y_wmin is the minimum value of Y coordinate of the window

(D) If bit 4 is "1" line intersects with the top boundary
                X_3=X1+(y-y₁)/m
                      where y = y_wmax
                y_wmax is the maximum value of Y coordinate of the window

Example of the Cohen-Sutherland Line Clipping Algorithm:

Leave R alone the rectangular window whose lower left-hand corner is at L (- 3, 1) and upper right-hand corner is at R (2, 6). Discover the district codes for the endpoints

The region code for point (x, y) is set according to the scheme
Bit 1 = sign (y-y_max)=sign (y-6)         Bit 3 = sign (x-x_max)= sign (x-2)
Bit 2 = sign (y_min-y)=sign(1-y)         Bit 4 = sign (x_min-x)=sign(-3-x)

So

                A (-4, 2)→ 0001         F (1, 2)→ 0000
                B (-1, 7) → 1000         G (1, -2) →0100
                C (-1, 5)→ 0000         H (3, 3) → 0100
                D (3, 8) → 1010         I (-4, 7) → 1001
                E (-2, 3) → 0000         J (-2, 10) → 1000

We place the line segments in their appropriate categories by testing the region codes found in the problem.

Category1 (visible): EF since the region code for both endpoints is 0000.

Category2 (not visible): IJ since (1001) AND (1000) =1000 (which is not 0000).

Category 3 (clipping case): AB since (0001) AND (1000) = 0000, CD since (0000) AND (1010) =0000, and GH. since (0100) AND (0010) =0000.

The candidates for clipping are AB, CD, and GH.

In cutting AB, the code for An is 0001. To push the 1 to 0, we cut against the limit line xmin=-3. The subsequent convergence point is I1 (- 3,3Line Clipping). We cut (don't show) AI1 and I1 B. The code for I1is 1001. The cut-out class for I1 B is 3 since (0000) AND (1000) is (0000). Presently B is outside the window (i.e., its code is 1000), so we push the 1 to a 0 by cutting against the line ymax=6. The subsequent crossing point is l2 (- 1Line Clipping,6). Consequently I2 B is cut. The code for I2 is 0000. The rest of the portion I1 I2 is shown since the two endpoints lie in the window (i.e., their codes are 0000). 

For cutting CD, we start with D since it is outside the window. Its code is 1010. We push the initial 1 to a 0 by cutting against the line ymax=6. The subsequent convergence I3 is (Line Clipping,6),and its code is 0000. Along these lines I3 D is cut and the rest of the portion CI3 has the two endpoints coded 0000 thus it is shown. 

For cutting GH, we can begin with either G or H since both are outside the window. The code for G is 0100, and we push the 1 to a 0 by cutting against the line ymin=1.The coming about crossing point is I4 (2Line Clipping,1) and its code is 0010. We cut GI4 and work on I4 H. Section I4 H isn't showing since (0010) AND (0010) =0010.

Next TopicCyrus-Beck Algorithm

← prevnext →